- Código: Selecionar Todos
a) 20 e 20 √3 b) 20 √3 e 20 c) 20 e 10√3 d) 10√3 e 20 e) n.d.a.
Podem ver nesta imagem como ficou o esquema:
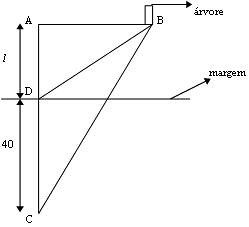
Ele se afastou (somente para trás) 40m, formando o angulo Ĉ que passou a valer 30°, com relação a posição da árvore. Antes a pessoa se encontrava em D, formando um ângulo de 60°.
Sabendo que a soma dos ângulos internos de um triângulo é 180. Se o ângulo do vértice D do triângulo ADB vale 60, o ângulo do D do DCB vale 120. Logo, o ângulo do B do triângulo DCB vale 180 - (120 + 30) = 30°. Logo, podemos constatar que o triângulo DCB é isósceles, tendo dois ângulos iguais, logo a semi-reta DB também é igual a 40m assim como DC.
Sabendo que no triângulo retângulo sen(α) = {cat. op.} / hip, e que o ângulo do B do triângulo ADB é 30.
Sabendo ainda que, sen(30) = 1/2. Podemos assim montar a proporção: 1 / 2 = l / 40.
Aplicando o produto dos meios pelo produto dos extremos temos: 2l = 40 → l = 40 / 2 → l = 20.
Logo, a largura do rio é igual a 20m. Mas, da altura da árvore, não entendi como resolver, podem me ajudar?


